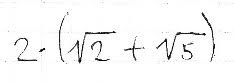Ci siamo.
Ricomincia la scuola, ricominciano i giochi. Matematici, s'intende.
La prof Giovanna ha pubblicato ieri sera, con un tempismo perfetto, i nuovi quesiti di Due a settimana..., è la puntata numero 16.
Fate clic sull'immagine qui sotto e scoprirete di cosa si tratta.
Sono due bei quesiti e, per come la vedo io, se presi per il verso giusto sono anche piuttosto facili.
Quindi mi aspetto risposte a profusione, un profluvio di risposte.
Entro il 15 aprile, mi raccomando.
giovedì 31 marzo 2016
martedì 22 marzo 2016
Sarà mica matematica 39, le soluzioni
Si tratta di cominciare.
Il primo passo è quello che conta. Solo dopo arriva il secondo, poi il terzo, poi... chissà fino a dove si può arrivare!
Ecco, queste possono sembrare frasi di grande saggezza (e un po' lo sono, per la verità). Ma sono soprattutto un modo per superare la mia pigrizia e iniziare questo post.
Questo era il primo passo.
Ora il secondo: spiegare qual è l'argomento del post. Si tratta delle soluzioni ai giochi di Sarà mica matematica 39.
Ora il terzo passo: illustrare le risposte cercando di dare un'ordine. L'ordine sarà il seguente: prima gli ospiti d'onore, poi le risposte giunte via mail - in rigoroso ordine di arrivo -, poi le risposte ben argomentate e consegnate su foglio di carta, infine le risposte cartacee corrette ma non spiegate.
Bene, se avete letto fino a qui, sapete che anche in questa puntata abbiamo un ospite d'onore! Si tratta di una mia ex-allieva, ora lanciata nel grande mare dell'università (il che gira il coltello nella piaga della mia crisi di mezza età avanzata)! La chiameremo semplicemente Caterina B, ma se volete potete conoscerla meglio dando un'occhiata al suo blog personale, La baita della tranquillità. Proprio così, Caterina ha un suo blog, dove parla soprattutto di libri. Lo voglio dire perché il fatto che qualcuno dei ggiovani si appassioni ancora alla lettura mi riconcilia un po' con il mondo.
Dunque possiamo cominciare con le soluzioni ai due quesiti? Cominciamo.
IL PRIMO
Il quesito partiva da questa immagine.
Si trattava di scoprire quanto vale ognuno dei tre simboli.
Caterina B, sostituisce cerchio, quadrato e triangolo con i simboli più usati in matematica per le incognite: X, Y e Z. Poi sfrutta le competenze acquisite al liceo, all'università (e - chissà - magari anche un po' alla scuola media...) per costruire un sistema di equazioni. È una robetta "semplice" e lei
la risolve in pochi passaggi.
Chi non ha, almeno ufficialmente, lo strumento "equazioni" deve faticare un po' di più. Vediamo allora come ce la siamo cavata noi delle scuole medie...
Il primo a rispondere è stato Edoardo O, il quale è sintetico, molto sintetico, troppo sintetico. Ecco la sua risposta, con un mio leggero ritocco dal punto di vista formale.
Altra mail, altro solutore. Si tratta di Stefano P, ecco cosa scrive.
Dato che il cerchio (C) si trova sia nella prima che nella seconda somma di numeri, la differenza tra queste è data solo dal passaggio da triangolo (T) a quadrato (Q).
Quindi la differenza tra quadrato e triangolo è: Q - T = 46 - 35 = 11.
Dato che ho la differenza e la somma di due numeri (Q - T = 11 e Q + T = 57), posso applicare la "regola":
Q = (somma + differenza) : 2 = (57 + 11) : 2 = 34
T = (somma - differenza) : 2 = (57 - 11) : 2 = 23.
Per trovare il cerchio basta fare C = 35 - T = 35 - 23 = 12.
Quindi alla fine ho: cerchio = 12, triangolo = 23, quadrato = 34.
Verifico il risultato:
12 + 23 = 35
34 + 12 = 46
23 + 34 = 57
Un paio di mail sono arrivate con soluzioni corrette ma senza spiegazioni. Quindi finiranno senza pietà in fondo alla fila, nel girone dei solutori non spiegatori.
Naomi R, invece manda un file in cui gioca, come suo solito, con le equazioni. Per mia comodità trasformo il suo scritto in Word in un'immagine:
La risposta di Davide C non è poi molto diversa.È arrivata su un foglio scritto a mano, le immagini che seguono sono una mia elaborazione. Le parole sono invece proprio quelle di Davide, riscritte da me con minime modifiche.
Francesco A trova la soluzione corretta, questo è certo. Altrettanto sicuro è che comincia piuttosto bene la sua discussione: scopre che la differenza tra quadrato e triangolo deve valere 11, così come la differenza tra triangolo e cerchio, mentre la differenza tra quadrato e cerchio vale 22.
Precisa anche che quadrato > triangolo > cerchio.
Poi però la sua spiegazione diventa incomprensibile, almeno per le mie povere capacità. Chissà, magari prossimamente trovererà il modo di spiegarmi cosa intendeva e potrò aggiornare questo post con la sua soluzione completa. Fino ad allora posso solo andare sulla fiducia.
Damanjot S e Cristian C (e, in maniera solo minimamente diversa anche Federico DM) arrivano alla soluzione giusta per una strada sbagliata. Sommano tutte le uguaglianze di partenza, poi dividono per 6 e trovano così che il triangolo vale 23.
Purtroppo però il risultato è giusto per puro caso.
Capita così solo perché avevo deciso di assegnare al cerchio il valore 12, al triangolo il valore 23 e al quadrato il valore 34.
In questa situazione si ha cerchio + quadrato = 46
Proprio come triangolo + triangolo = 46
Quindi sommando tutte le figure è come se sommassi 6 triangoli.
Ma cosa succederebbe se il cerchio valesse, che so, e 10 e il quadrato 30? I conti non tornerebbero più, provare per credere!
Hanno fornito la risposta corretta ma non hanno spiegato (un po' come dire che non hanno veramente risposto!): Alessia S, Aurora R, Chiara e Paolo M, Mattia C, Morgana M, Sara T, Viola Q.
Nessuno qui ha individuato la soluzione suggerita dal libro di mio figlio, da cui avevo preso spunto per il quesito. Tento di farlo io.
Sommando tutte le uguaglianze di partenza si ha
Il primo passo è quello che conta. Solo dopo arriva il secondo, poi il terzo, poi... chissà fino a dove si può arrivare!
Ecco, queste possono sembrare frasi di grande saggezza (e un po' lo sono, per la verità). Ma sono soprattutto un modo per superare la mia pigrizia e iniziare questo post.
Questo era il primo passo.
Ora il secondo: spiegare qual è l'argomento del post. Si tratta delle soluzioni ai giochi di Sarà mica matematica 39.
Ora il terzo passo: illustrare le risposte cercando di dare un'ordine. L'ordine sarà il seguente: prima gli ospiti d'onore, poi le risposte giunte via mail - in rigoroso ordine di arrivo -, poi le risposte ben argomentate e consegnate su foglio di carta, infine le risposte cartacee corrette ma non spiegate.
Bene, se avete letto fino a qui, sapete che anche in questa puntata abbiamo un ospite d'onore! Si tratta di una mia ex-allieva, ora lanciata nel grande mare dell'università (il che gira il coltello nella piaga della mia crisi di mezza età avanzata)! La chiameremo semplicemente Caterina B, ma se volete potete conoscerla meglio dando un'occhiata al suo blog personale, La baita della tranquillità. Proprio così, Caterina ha un suo blog, dove parla soprattutto di libri. Lo voglio dire perché il fatto che qualcuno dei ggiovani si appassioni ancora alla lettura mi riconcilia un po' con il mondo.
Dunque possiamo cominciare con le soluzioni ai due quesiti? Cominciamo.
IL PRIMO
Il quesito partiva da questa immagine.
Si trattava di scoprire quanto vale ognuno dei tre simboli.
Caterina B, sostituisce cerchio, quadrato e triangolo con i simboli più usati in matematica per le incognite: X, Y e Z. Poi sfrutta le competenze acquisite al liceo, all'università (e - chissà - magari anche un po' alla scuola media...) per costruire un sistema di equazioni. È una robetta "semplice" e lei
la risolve in pochi passaggi.
Chi non ha, almeno ufficialmente, lo strumento "equazioni" deve faticare un po' di più. Vediamo allora come ce la siamo cavata noi delle scuole medie...
Il primo a rispondere è stato Edoardo O, il quale è sintetico, molto sintetico, troppo sintetico. Ecco la sua risposta, con un mio leggero ritocco dal punto di vista formale.
57+46-35=103-35=68
68:2=34(un quadrato)
46-34=12(un cerchio)
35-12=23(un triangolo)
Il ragionamento di Edoardo rimane un po' criptico ma con un pizzico di attenzione è facile notare come il procedimento sia quasi identico a quello di Caterina!
Altra mail, altro solutore. Si tratta di Stefano P, ecco cosa scrive.
Dato che il cerchio (C) si trova sia nella prima che nella seconda somma di numeri, la differenza tra queste è data solo dal passaggio da triangolo (T) a quadrato (Q).
Quindi la differenza tra quadrato e triangolo è: Q - T = 46 - 35 = 11.
Dato che ho la differenza e la somma di due numeri (Q - T = 11 e Q + T = 57), posso applicare la "regola":
Q = (somma + differenza) : 2 = (57 + 11) : 2 = 34
T = (somma - differenza) : 2 = (57 - 11) : 2 = 23.
Per trovare il cerchio basta fare C = 35 - T = 35 - 23 = 12.
Quindi alla fine ho: cerchio = 12, triangolo = 23, quadrato = 34.
Verifico il risultato:
12 + 23 = 35
34 + 12 = 46
23 + 34 = 57
Un paio di mail sono arrivate con soluzioni corrette ma senza spiegazioni. Quindi finiranno senza pietà in fondo alla fila, nel girone dei solutori non spiegatori.
Naomi R, invece manda un file in cui gioca, come suo solito, con le equazioni. Per mia comodità trasformo il suo scritto in Word in un'immagine:
La risposta di Davide C non è poi molto diversa.È arrivata su un foglio scritto a mano, le immagini che seguono sono una mia elaborazione. Le parole sono invece proprio quelle di Davide, riscritte da me con minime modifiche.
Per prima cosa ho ottenuto il valore di ogni figura "ribaltando" le uguaglianze iniziali.
Ho preso la prima uguaglianza e ho cercato di trasformarla sostituendo le figure con le arie uguaglianze, in modo da lasciare una sola incognita.
Ismaele M ha risolto in maniera molto simile (anche lui ha scritto a mano e non ho intenzione di riscrivere tutto!). Ha individuato bene il valore del triangolo. Peccato abbia poi dimenticato gli ultimi passaggi, i più facili: non scrive quanto valgono il cerchio e il quadrato!
Mi è piaciuta la soluzione di Nelson R, il quale non usa equazioni, nemmeno sotto false spoglie. In prima media, ne ha tutto il diritto. Sceglie invece una strada più originale.
Ho notato che tra le somme c'è sempre una differenza di 11.
Quindi se faccio (35 + 11):2 ottengo 23 che è il valore o del cerchio o del triangolo. Se al totale 35 tolgo poi 23 ottengo 12 che è il valore dell'altra figura.
Ora faccio lo stesso per la terza coppia, cioè (57 +11):2. Esce 34. Se lo sottraggo a 57 risulta 23.
Quindi ho capito che il 23 si ripete nella prima e nella terza coppia. Perciò è il triangolo.
Nella prima coppia rimane 12, che è il valore del cerchio.
L'ultimo valore che resta è 34, cioè il quadrato.
Dopodiché ho sostituito il valore del triangolo nelle uguaglianze iniziali per trovare il valore di cerchio e quadrato.
Ismaele M ha risolto in maniera molto simile (anche lui ha scritto a mano e non ho intenzione di riscrivere tutto!). Ha individuato bene il valore del triangolo. Peccato abbia poi dimenticato gli ultimi passaggi, i più facili: non scrive quanto valgono il cerchio e il quadrato!
Ho notato che tra le somme c'è sempre una differenza di 11.
Quindi se faccio (35 + 11):2 ottengo 23 che è il valore o del cerchio o del triangolo. Se al totale 35 tolgo poi 23 ottengo 12 che è il valore dell'altra figura.
Ora faccio lo stesso per la terza coppia, cioè (57 +11):2. Esce 34. Se lo sottraggo a 57 risulta 23.
Quindi ho capito che il 23 si ripete nella prima e nella terza coppia. Perciò è il triangolo.
Nella prima coppia rimane 12, che è il valore del cerchio.
L'ultimo valore che resta è 34, cioè il quadrato.
Francesco A trova la soluzione corretta, questo è certo. Altrettanto sicuro è che comincia piuttosto bene la sua discussione: scopre che la differenza tra quadrato e triangolo deve valere 11, così come la differenza tra triangolo e cerchio, mentre la differenza tra quadrato e cerchio vale 22.
Precisa anche che quadrato > triangolo > cerchio.
Poi però la sua spiegazione diventa incomprensibile, almeno per le mie povere capacità. Chissà, magari prossimamente trovererà il modo di spiegarmi cosa intendeva e potrò aggiornare questo post con la sua soluzione completa. Fino ad allora posso solo andare sulla fiducia.
Damanjot S e Cristian C (e, in maniera solo minimamente diversa anche Federico DM) arrivano alla soluzione giusta per una strada sbagliata. Sommano tutte le uguaglianze di partenza, poi dividono per 6 e trovano così che il triangolo vale 23.
Purtroppo però il risultato è giusto per puro caso.
Capita così solo perché avevo deciso di assegnare al cerchio il valore 12, al triangolo il valore 23 e al quadrato il valore 34.
In questa situazione si ha cerchio + quadrato = 46
Proprio come triangolo + triangolo = 46
Quindi sommando tutte le figure è come se sommassi 6 triangoli.
Ma cosa succederebbe se il cerchio valesse, che so, e 10 e il quadrato 30? I conti non tornerebbero più, provare per credere!
Nessuno qui ha individuato la soluzione suggerita dal libro di mio figlio, da cui avevo preso spunto per il quesito. Tento di farlo io.
Sommando tutte le uguaglianze di partenza si ha
Tale somma contiene due cerchi, due triangoli e due quadrati. Perciò dividendo per due si ottiene la somma dei tre simboli.
Per scoprire il valore di ciascun simbolo basta poi fare delle sottrazioni.
Un suggerimento: andate tutti a dare un occhiata - anzi, direi a leggere con attenzione! - le risposte sul blog della prof Giovanna. Almeno quattro diversi ragazzi hanno scoperto, con qualche minima variazione, proprio questa soluzione. Certo, può darsi che abbiano anche loro lo stesso libro di testo di mio figlio. Però ne dubito.
A buon intenditor, poche parole! O, se preferite: chi ha orecchie per intendere intenda!
Per scoprire il valore di ciascun simbolo basta poi fare delle sottrazioni.
Un suggerimento: andate tutti a dare un occhiata - anzi, direi a leggere con attenzione! - le risposte sul blog della prof Giovanna. Almeno quattro diversi ragazzi hanno scoperto, con qualche minima variazione, proprio questa soluzione. Certo, può darsi che abbiano anche loro lo stesso libro di testo di mio figlio. Però ne dubito.
A buon intenditor, poche parole! O, se preferite: chi ha orecchie per intendere intenda!
IL SECONDO
Ritroviamo Caterina B, la nostra ospite!
Caterina va subito sul complicato e calcola il perimetro della freccia applicando il teorema di Pitagora.
Mattia C, nella sua mail, pasticcia un po' (un bel po', in effetti) con il teroema di Pitagora. In qualche modo riesce però a scoprire l'area della freccia (ma attenzione, Mattia: l freccia NON è formata da due triangoli rettangoli isosceli!). Sbaglia invece il perimetro. Ma è in prima e non sapere il teorema di Pitagora gli è più che concesso.
Alessia S invia la foto di un foglio con il calcolo dell'area e del perimetro. Entrambi sono corretti ma la foto è storta e di scarsa qualità. Purtroppo Alessia non è l'ospite d'onore, quindi, come detto, non farò lavori di ritocco fotografico. Se volete sapere il ragionamento seguito da Alessia chiedete direttamente a lei... :-)
Naomi R, come suo solito, manda una mail con delle risposte complete e ben scritte. Stavolta però ha troppa fretta e... sbaglia ad applicare il teorema di Pitagora! (Serve la somma dei cateti, non il prodotto!). Peccato.
Tutte le altre risposte sono scritte a mano (in alcuni casi dovrei dire scarabocchiate a mano!). Da qui in poi, quindi, andremo veloci.
C'è chi nota che il quairato è suddiviso in quattro parti: tre triangoli bianchi e la freccia arancione.
Quindi calcola l'area della freccia sottraendo all'area del quadrato l'area dei tre triangoli.
Scelgono questa strada: Andrea G, Ismaele M, Luca N e Nicolò A, Mattia C, Viola Q. Lo stesso vale anche per Davide C e per Lorenzo B, i quali complicano solo un po' le cose.
C'è chi calcola l'area del triangolo ADE e sottrae l'area del triangolo ADF.
Seguono questa strada: Aurora R, Chiara e Paolo M, Francesco A, Sara T .
Per calcolare il perimetro tutti fanno quel che ha fatto Stefano P (vedi sopra). Nessuno (e quando dico nessuno intendo proprio nessuno) però sceglie la soluzione elegante e precisa di lasciare indicate le radici. Tutti calcolano. Naturalmente gli arrotondamenti sono scelti secondo il gusto personale. Quindi i risultati finali sono piuttosto variabili: si va da 7 fino a 7,31 cm2.
Poi dicono che la matematica non è un'opinione!
I nomi dei calcolatori: Andrea G, Aurora R, Chiara e Paolo M, Cristian C e Damanjot S, Francesco A, Ismaele M, Luca N e Nicolò A, Mattia C, Sara , Viola Q.
Bene, passo dopo passo, siamo arrivati in fondo anche stavolta.
Ho la strana sensazione di dimenticare qualcosa ma forse è solo stanchezza.
Mi complimento, come sempre, con tutti quelli che ci hanno provato, riuscendoci o meno. Sono anche quelli che si troveranno con i muscoli del cervello più robusti. Il fatto che il cervello non abbia muscoli è del tutto irrilevante!
Chiudiamo questa puntata con un augurio di buone feste pasquali.
Al ritorno ci troveremo tutti dalla prof Giovanna per i nuovi quesiti di Due a settimana...
Ritroviamo Caterina B, la nostra ospite!
Caterina va subito sul complicato e calcola il perimetro della freccia applicando il teorema di Pitagora.
Poi trova il perimetro di uno dei due triangoli che formano la freccia.
Infine va sul più complicato ancora! Calcola l'area con la formula di Erone!
A questo punto devo fare un paio di precisazioni.
Caterina ha evidentemente risolto il problema nelle pause tra una studiata e l'altra. Dopodiché mi ha inviato un paio di foto del suo blocco degli appunti. La mia opera di riassemblaggio delle immagini, per quanto non particolarmente accurata, è un trattamento di favore, riservato solo all'ospite d'onore...!
La strada scelta da Caterina è fuori dalla portata di tutti i miei alunni attuali. O perché non conoscono ancora il teorema di Pitagora o perché non abbiamo visto la formula di Erone. Non è un caso che io avessi chiesto per prima cosa l'area della freccia.
Torniamo allora alle scuole medie attuali. E vediamo come risponde Edoardo O, anche stavolta sintetico fino all'eccesso, tanto che tralascia di dare la risposta finale!. Ad ogni modo il suo ragionamento resta valido. Edoardo, essendo in prima, si limita a determinare l'area della freccia. Fa riferimento alla figura originale:
Infine va sul più complicato ancora! Calcola l'area con la formula di Erone!
A questo punto devo fare un paio di precisazioni.
Caterina ha evidentemente risolto il problema nelle pause tra una studiata e l'altra. Dopodiché mi ha inviato un paio di foto del suo blocco degli appunti. La mia opera di riassemblaggio delle immagini, per quanto non particolarmente accurata, è un trattamento di favore, riservato solo all'ospite d'onore...!
La strada scelta da Caterina è fuori dalla portata di tutti i miei alunni attuali. O perché non conoscono ancora il teorema di Pitagora o perché non abbiamo visto la formula di Erone. Non è un caso che io avessi chiesto per prima cosa l'area della freccia.
Torniamo allora alle scuole medie attuali. E vediamo come risponde Edoardo O, anche stavolta sintetico fino all'eccesso, tanto che tralascia di dare la risposta finale!. Ad ogni modo il suo ragionamento resta valido. Edoardo, essendo in prima, si limita a determinare l'area della freccia. Fa riferimento alla figura originale:
ABE+ECD=1/4 ABCD+1/4 ABCD=2/4 ABCD
2/4 ABCD+ AFD= 2/4 ABCD+1/4 ABCD=3/4 ABCD
Parte colorata=Area ABCD-3/4 ABCD=4/4 ABCD-3/4 ABCD=1/4 ABCD
L’area della parte colorata è uguale a un quarto dell’area del quadrato.
2/4 ABCD+ AFD= 2/4 ABCD+1/4 ABCD=3/4 ABCD
Parte colorata=Area ABCD-3/4 ABCD=4/4 ABCD-3/4 ABCD=1/4 ABCD
L’area della parte colorata è uguale a un quarto dell’area del quadrato.
Anche Stefano P manda una mail in cui, sempre riferendosi alla figura sopra, scrive:
Per trovare l'area della freccia considero l'area del triangolo ADE e faccio (base x altezza) : 2 = (2 x 2) : 2 = 2cm2.
Per trovare l'area della freccia considero l'area del triangolo ADE e faccio (base x altezza) : 2 = (2 x 2) : 2 = 2cm2.
Poi sottraggo l'area del triangolo ADF che è (2 x 1) : 2 = 1cm2.
Quindi l'area della freccia è 2cm2 - 1cm2 = 1cm2.
Per trovare il perimetro invece trovo prima il lato AE con il teorema di Pitagora
Poi trovo AF che è la metà della diagonale del quadrato facendo
Infine raddoppio questi due lati per trovare il perimetro totale che è
Complimenti a Stefano per aver ascoltato quello che ci siamo detti e ridetti a lezione e quindi NON aver calcolato le radici.
Poi trovo AF che è la metà della diagonale del quadrato facendo
Infine raddoppio questi due lati per trovare il perimetro totale che è
Complimenti a Stefano per aver ascoltato quello che ci siamo detti e ridetti a lezione e quindi NON aver calcolato le radici.
Mattia C, nella sua mail, pasticcia un po' (un bel po', in effetti) con il teroema di Pitagora. In qualche modo riesce però a scoprire l'area della freccia (ma attenzione, Mattia: l freccia NON è formata da due triangoli rettangoli isosceli!). Sbaglia invece il perimetro. Ma è in prima e non sapere il teorema di Pitagora gli è più che concesso.
Alessia S invia la foto di un foglio con il calcolo dell'area e del perimetro. Entrambi sono corretti ma la foto è storta e di scarsa qualità. Purtroppo Alessia non è l'ospite d'onore, quindi, come detto, non farò lavori di ritocco fotografico. Se volete sapere il ragionamento seguito da Alessia chiedete direttamente a lei... :-)
Naomi R, come suo solito, manda una mail con delle risposte complete e ben scritte. Stavolta però ha troppa fretta e... sbaglia ad applicare il teorema di Pitagora! (Serve la somma dei cateti, non il prodotto!). Peccato.
Tutte le altre risposte sono scritte a mano (in alcuni casi dovrei dire scarabocchiate a mano!). Da qui in poi, quindi, andremo veloci.
C'è chi nota che il quairato è suddiviso in quattro parti: tre triangoli bianchi e la freccia arancione.
Quindi calcola l'area della freccia sottraendo all'area del quadrato l'area dei tre triangoli.
Scelgono questa strada: Andrea G, Ismaele M, Luca N e Nicolò A, Mattia C, Viola Q. Lo stesso vale anche per Davide C e per Lorenzo B, i quali complicano solo un po' le cose.
C'è chi calcola l'area del triangolo ADE e sottrae l'area del triangolo ADF.
Seguono questa strada: Aurora R, Chiara e Paolo M, Francesco A, Sara T .
Per calcolare il perimetro tutti fanno quel che ha fatto Stefano P (vedi sopra). Nessuno (e quando dico nessuno intendo proprio nessuno) però sceglie la soluzione elegante e precisa di lasciare indicate le radici. Tutti calcolano. Naturalmente gli arrotondamenti sono scelti secondo il gusto personale. Quindi i risultati finali sono piuttosto variabili: si va da 7 fino a 7,31 cm2.
Poi dicono che la matematica non è un'opinione!
I nomi dei calcolatori: Andrea G, Aurora R, Chiara e Paolo M, Cristian C e Damanjot S, Francesco A, Ismaele M, Luca N e Nicolò A, Mattia C, Sara , Viola Q.
Bene, passo dopo passo, siamo arrivati in fondo anche stavolta.
Ho la strana sensazione di dimenticare qualcosa ma forse è solo stanchezza.
Mi complimento, come sempre, con tutti quelli che ci hanno provato, riuscendoci o meno. Sono anche quelli che si troveranno con i muscoli del cervello più robusti. Il fatto che il cervello non abbia muscoli è del tutto irrilevante!
Chiudiamo questa puntata con un augurio di buone feste pasquali.
Al ritorno ci troveremo tutti dalla prof Giovanna per i nuovi quesiti di Due a settimana...
venerdì 4 marzo 2016
Sarà mica matematica 39
Anzi, sapete cosa vi dico? Non perdiamo tempo in chiacchiere e passiamo subito ai quesiti (e anche nei quesiti sprecheremo poco tempo in ciance).
IL PRIMO
C'è una prima volta per tutto e questa è una prima volta.
Butto lì un quesito senza parole. Per la prima volta.
Mi permetto solo di aggiungere che, dal momento che ho rubato l'idea dal libro di scuola di mio figlio, non dovrebbe essere un problema di difficoltà insormontabile.
IL SECONDO
Siccome mi sento generoso voglio esagerare: vi offro due immagini al prezzo di una. Una animata e una fissa. No, no, non serve che mi rigraziate.
L'immagine animata può servire per capire meglio la costruzione.
L'immagine fissa torna più utile per ragionarci sopra.
Adesso però staccate gli occhi e leggete il testo del quesito: ABCD è un quadrato di lato 2 cm. E è il punto medio di BC. F è il punto di intersezione tra le diagonali del quadrato.
Quanto è l'area della "freccia" arancione?
Per secondini e terzini oso perfino chiedere il perimetro della freccia!
E con questo sono finiti i quesiti. Una puntata all'insegna della velocità!
Voi però prendetevi il tempo necessario per pensare e, dopo aver ragionato, rispondete con la dovuta calma e precisione.
Come al solito avete ben due settimane a disposizione (la scadenza è venerdì 18 marzo 2016).
Più di così...
Iscriviti a:
Post (Atom)