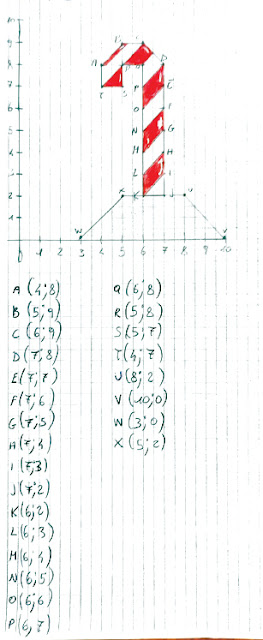
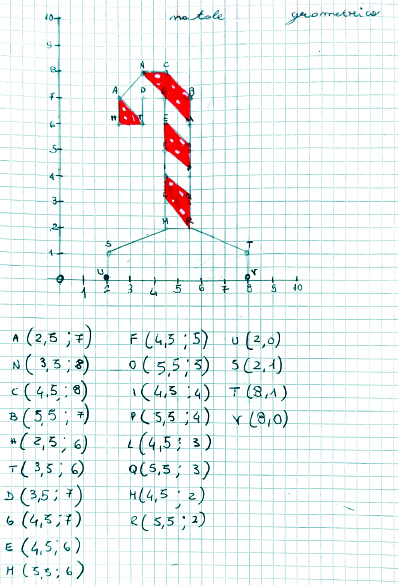
Questo blog sembra deceduto, lo so. Forse lo è anche, chissà. Ad ogni modo torna vivo per l'occasione. Il penultimo giorno di scuola ho proposto alla prima A un concorso a premi SENZA premi: classe divisa sui tavoloni, come sempre; ogni gruppo realizza tre disegni natalizi sul piano cartesiano e ne seleziona uno (o al massimo due); si vota per eleggere il migliore.
Giuro che non ricordo più qual è quello che ha vinto. Ma poco importa, credo che i complimenti vadano a tutta la classe, per come ha raccolto la proposta, per l'impegno con cui tutti hanno lavorato... bravi!
Come (piccolo!) regalo di Natale ho deciso di riattivare Un tesoro in ogni dove per pubblicare le vostre creazioni, ragazze e ragazzi. Lo faccio in ritardo, nel rispetto della tradizione del blog.
Pronti? Ecco una carrellata delle undici opere d'arte. Controllate voi che le coordinate siano corrette?